고유값과 고유벡터
고유값과 고유벡터는 앞서 활용한 공분산행렬, 그리고 앞에 설명할 주성분 분석과 뗄 수 없는 관계이다. 따라서 PCA의 메커니즘을 제대로 이해하기 위해서는 고유값과 고유벡터가 의마하는 바를 제대로 이해하는 게 좋다.
고유값과 고유벡터 설명
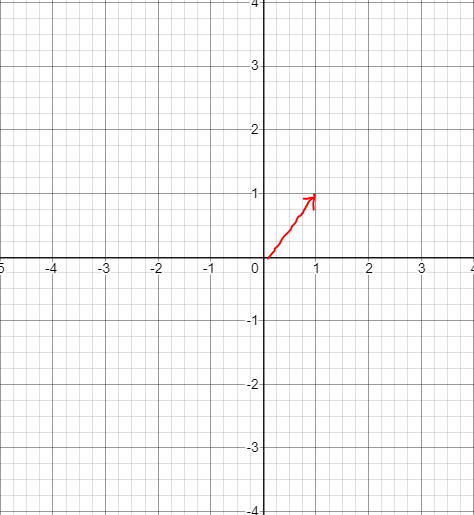
$$X=\begin{bmatrix} 1 \\ 1 \end{bmatrix}$$ 이라는 행렬이 있다고 가정해보자. 이 행렬에 만약 $$A=\begin{bmatrix} 2&1 \\ 1&2 \end{bmatrix}$$를 선형변환하면 이렇게 계산할 수 있다.
- $$AX= \begin{bmatrix} 2&1 \\ 1&2 \end{bmatrix}\begin{bmatrix} 1 \\ 1 \end{bmatrix}=\begin{bmatrix} 3 \\ 3 \end{bmatrix}$$
즉 어떤 벡터에 A를 곱하니 벡터의 방향은 그대로이고 길이만 변하였다고 표현할 수 있다. 다시 말하면 아래 좌표평면에 있는 (1,1) 벡터가 (3,3)가지 방향의 변환 없이 그대로 이동한 것이다.
여기서 $$AX = \lambda X$$ 가 되는 $$\lambda$$ 값이 바로 고유값(eigen value)이다. 조금 더 정리를 해보자
- $$AX - \lambda IX = (A - \lambda I)X = 0$$
- $$det(A - \lambda I) = 0$$ (det는 determinant이며, $$ad-bc$$의 형태로 행렬값을 계산하는 수식임)
- $$det(A - \lambda I) = det\begin{bmatrix} 2-\lambda&1 \\ 1&2-\lambda \end{bmatrix} = 0$$
- $$(2-\lambda)^2 -1 = (\lambda-1)(\lambda-3) = 0 $$
- $$\lambda =2$$ or $$\lambda =3$$
- 즉 고유값은 2 또는 3이다
그럼 여기서 고유벡터를 구하면 아래와 같이 볼 수 있다
- 고유값이 3인 경우, $$\begin{bmatrix} 2&1 \\ 1&2 \end{bmatrix}\begin{bmatrix} X_1 \\ X_2 \end{bmatrix} = 3\begin{bmatrix} X_1 \ X_2 \end{bmatrix}$$
- $$2X_1 + X_2 = 3X_1$$
- $$X_1 + 2X_2 = 3X_2$$
- $$X_1 = X_2$$
- 가장 쉬운 형태의 고유행렬로 $$\begin{bmatrix} X_1 \\ X_2 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} $$로 볼 수 있다.
- 고유값이 1인 경우도 동일하게 구할 수 있다
고유값과 고유벡터의 의미
$$A$$ 행렬을 공분산 행렬(covariance matrix)이라고 생각해보자.
- $$\begin{bmatrix} 2&1 \\ 1&2 \end{bmatrix}$$ 행렬의 고유값은 1과 3이다
- 고유값의 합은 4로, 두 분산의 합(2+2)과 같다
- 고유값의 곱은 $$det(A) = (2_2 - 1_1)$$과 동일
- 분산정보는 최대한 해치지 않으면서 차원을 축소하기 위해 고유값과 고유벡터를 찾아낸 것
- 고유벡터는 행렬 A를 곱하더라도 방향이 변하지 않고 그 크기만 변하는 벡터를 의미함
주성분 분석(PCA)
주성분 분석의 목적
주성분 분석의 목적 및 핵심은 아래와 같다.
- 고차원의 데이터를 저차원으로 줄이는 것
- 공통된 변수들을 줄여서 주성분을 찾는 것
- 사용된 변수의 개수 > 주성분의 개수
- 하지만 전체 데이터의 분산에 영향을 주어서는 안됨
주성분 뽑아낼 때 원칙
분산이 가장 커지는 축을 첫 번째 주성분으로 두고, 그 다음 분산이 두번째로 커지는 축을 두 번째 주성분으로 두는 식으로 주성분은 추출
각 주성분은 서로간 90도 직교함
- 공분산 행렬의 고유벡터 개념임
위에서 고유값 3일 때 계산되는 첫 번째 고유벡터가 바로 첫 번째 주성분(PC1)이 된다. 즉, $$ \begin{bmatrix} 1 \ 1 \end{bmatrix} $$ 고유벡터가 첫 번째 주성분 축이 된다는 의미임
원본 데이터가 있을 경우 먼저 표준화가 진행된다
표준화가 되었다고 가정하고, $$ \begin{bmatrix} 70&80 \\ 50&40 \\ 70&90 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} $$ 이 계산 되어 최종 $$\begin{bmatrix} 150 \\ 90 \\ 160 \end{bmatrix} $$이 되어 새로운 축으로 반영되는 것이다. 이 축은 국어와 영어점수를 설명하는 '언어능력점수' 정도로 해석해 볼 수 있다.
2차원 좌표평면에서 설명해야 이해가 빠른데, 해당 설명은 참고유튜브를 참조하자
고유값이 1일 때 나왔던 주성분 PC2(고유벡터)는 분산의 설명도에 따라 사용할 수도, 안 할 수도 있다
PC1과 PC2의 상관관계는 0이다(고유값의 계산관계 상 0이 될 수 밖에 없다.)
주성분 분석을 사용할 때
- 주성분 분석은 언제나 가능한가?
- 주성분 분석은 데이터의 이면에 보이지 않는 원인이 있음을 전제
- 즉 국어점수와 영어점수를 설명하는 '언어능력'이 있음을 생각하는 것
- 주성분 분석에 적합한 데이터란 무엇인가?
- 구형성 검증(Bartlett's test of sphericity)
- "상관관계가 0이라면 주성분이 존재할 수 있는가?"를 생각하는 것
- 즉 상관관계가 업는 형태라면 주성분 분석을 할 수 없음
PCA 실습
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns # seaborn
import warnings
warnings.filterwarnings("ignore") # 경고메세지 무시
df = pd.read_excel("./data/pca_credit_card/card.xls", header=1).iloc[:,1:]print(df.shape)
df.head(3)(30000, 24)| LIMIT_BAL | SEX | EDUCATION | MARRIAGE | AGE | PAY_0 | PAY_2 | PAY_3 | PAY_4 | PAY_5 | ... | BILL_AMT4 | BILL_AMT5 | BILL_AMT6 | PAY_AMT1 | PAY_AMT2 | PAY_AMT3 | PAY_AMT4 | PAY_AMT5 | PAY_AMT6 | default payment next month | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 20000 | 2 | 2 | 1 | 24 | 2 | 2 | -1 | -1 | -2 | ... | 0 | 0 | 0 | 0 | 689 | 0 | 0 | 0 | 0 | 1 |
| 1 | 120000 | 2 | 2 | 2 | 26 | -1 | 2 | 0 | 0 | 0 | ... | 3272 | 3455 | 3261 | 0 | 1000 | 1000 | 1000 | 0 | 2000 | 1 |
| 2 | 90000 | 2 | 2 | 2 | 34 | 0 | 0 | 0 | 0 | 0 | ... | 14331 | 14948 | 15549 | 1518 | 1500 | 1000 | 1000 | 1000 | 5000 | 0 |
3 rows × 24 columns
default payment next month가 Target 이며 1이면 "다음달 연체", 0이면 "정상납"임
df.rename(columns={"PAY_0":"PAY_1", "default payment next month":"default"}, inplace=True)
y_target = df["default"]
X_features = df.drop("default", axis=1)corr = X_features.corr()
plt.figure(figsize=(14,14))
sns.heatmap(corr, annot=True, fmt='.1g')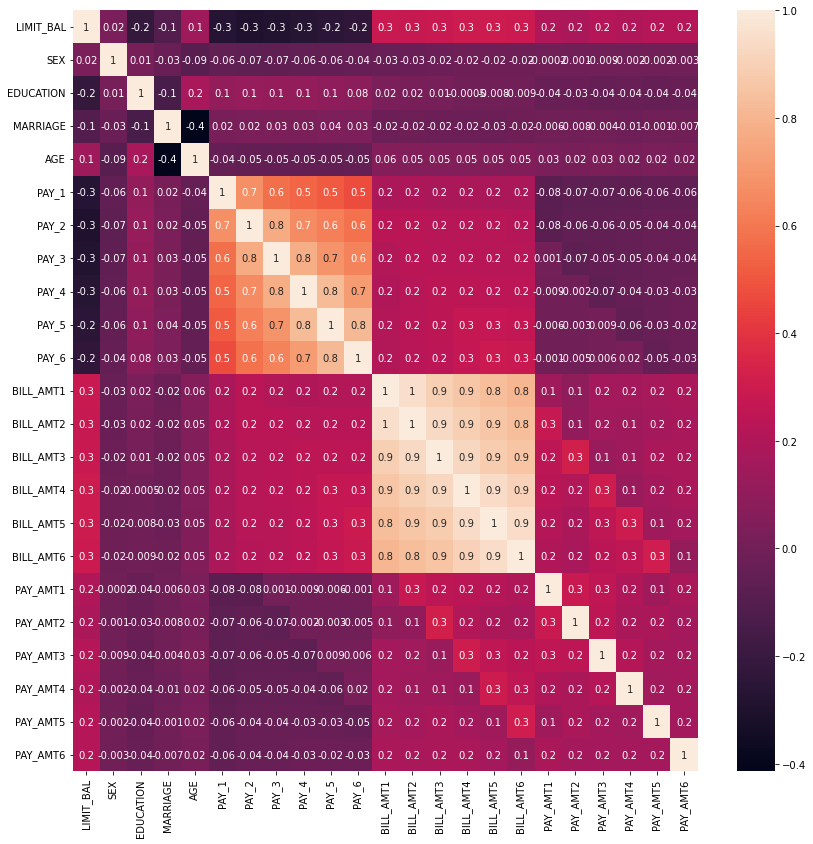
- PAY_1 ~ 6까지의 상관도와 BILL_AMT1 ~ 6까지의 상관도가 각각 높음
- PCA로 변환을 시행
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
# BILL
cols_bill = ["BILL_AMT" + str(i) for i in range(1,7)]
print("대상 속성명 :", cols_bill)
# PCA 객체 생성 후 변환
scaler = StandardScaler()
df_cols_scaled = scaler.fit_transform(X_features[cols_bill])
pca = PCA(n_components=2)
pca.fit(df_cols_scaled)
print("PCA Component 별 변동성 :", pca.explained_variance_ratio_)대상 속성명 : ['BILL_AMT1', 'BILL_AMT2', 'BILL_AMT3', 'BILL_AMT4', 'BILL_AMT5', 'BILL_AMT6']
PCA Component 별 변동성 : [0.90555253 0.0509867 ]from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score
rcf = RandomForestClassifier(n_estimators=300, random_state=156)
scores = cross_val_score(rcf, X_features, y_target, scoring="accuracy", cv=3)
print("개별 정확도 :", scores)
print("평균정확도:", np.round(np.mean(scores),3))개별 정확도 : [0.8083 0.8196 0.8232]
평균정확도: 0.817# 원본 데이터 세트에 먼저 StandardScaler
scaler = StandardScaler()
df_scaled = scaler.fit_transform(X_features)
# 6개의 컴포넌트를 가진 PCA 변환 수행 cross_val_score()로 분류 예측 수행
pca = PCA(n_components=6)
df_pca = pca.fit_transform(df_scaled)
scores_pca = cross_val_score(rcf, df_pca, y_target, scoring="accuracy", cv=3)
print("개별 정확도 :", scores_pca)
print("평균정확도:", np.round(np.mean(scores_pca),3))개별 정확도 : [0.7905 0.7976 0.8021]
평균정확도: 0.797# 6개의 변수만으로도 성능의 차이가 크게 없음
pca.explained_variance_ratio_array([0.28448215, 0.17818817, 0.06743307, 0.06401153, 0.04457547,
0.04161736])- 결론적으로 PCA를 사용할 때는 변수가 많고, X변수 간의 상관관계가 있다 싶을 때 사용한다
- 그리고 원본 데이터를 돌려보고 시간이 많이 걸린다 싶을 때 차원 축소를 고려해볼 수 있다
- 대신 각 변수의 해석의 문제가 남는다.
'Data > Machine Learning' 카테고리의 다른 글
| 경사하강법(Gradient Decent) 정리 (0) | 2022.04.12 |
|---|---|
| 차원축소(Dimension Reduction) 정리 (0) | 2022.04.12 |
| Rigdge와 Lasso (0) | 2022.03.31 |
| Decision Tree Regression (0) | 2019.12.27 |
| 파이썬 사이킷런에서 model에서 fit and fit_transform의 차이 (0) | 2019.09.28 |