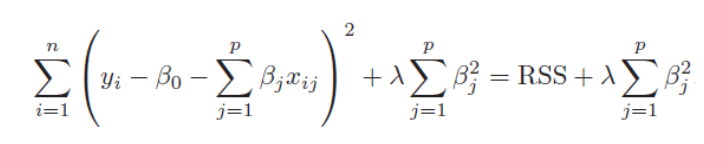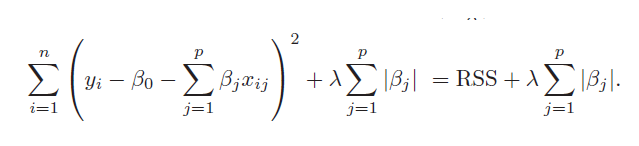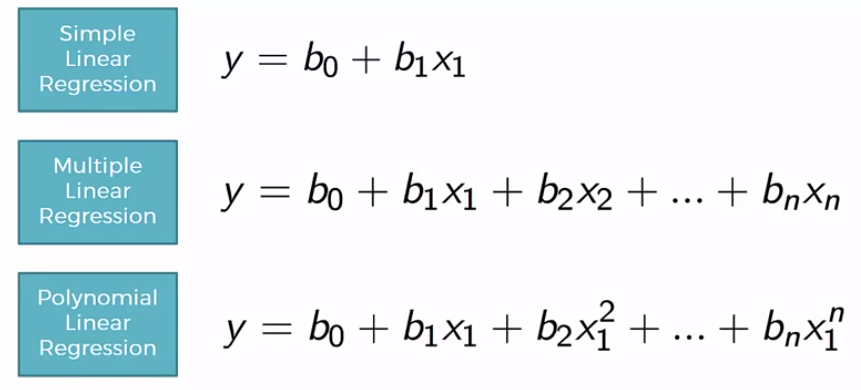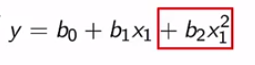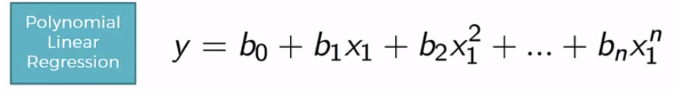경사하강법 정의
경사 하강법(傾斜下降法, Gradient descent)은 1차 근삿값 발견용 최적화 알고리즘이다. 기본 개념은 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것이다
위키피디아
이 개념을 숙지하기 위해서는 비용함수라는 개념을 먼저 알아두면 좋다.
비용함수
$$y = w_1*x_1 + w_0$$ 라는 회귀식이 있을 경우, 이 함수의 *_비용함수 RSS**는 다음과 같다. (약간의 회귀분석에 대한 개념이 필요)
$$RSS(w_0, w_1) = \frac{1}{N}\sum_{i=1}^{N}(y_i-(w_0+w_1*x_i))^2$$
여기서 N은 학습데이터의 총 건수이며, i는 각 데이터포인트이다. 회귀에서는 이 RSS는 비용이라고 하며 w변수로 구성되는 RSS를 비용함수, 또는 손실함수(loss function)라고 한다. 머신러닝 회귀 알고리즘에서는 데이터를 계속 학습하면서 이 비용함수가 반환되는 값을 지속해서 감소시키고, 최종적으로는 더이상 감소하지 않는 최소의 오류값을 구하고자 한다.
오류값을 지속해서 작아지게 하는 방향으로 W값을 계속 업데이트해 나가며, 오류값이 더 이상 작아지지 않으면 그 오류값을 최소 비용으로 판단하고 그 W를 최적의 파라미터로 판단한다.
머신러닝에서 쓰이는 이유
그럼 비용함수가 최소가 되는 W파라미터를 어떻게 구할 수 있을까? 하는 대답에 경사하강법이 사용되는 것이다. 모든 변수(x)를 미분하여 최소값을 가지는 계수를 찾아내는 방법이 있을 수 있으나 아래의 이유로 경사하강법이 쓰인다.
- 실제 분석에서는 함수의 형태가 복잡하므로 미분계수와 그 근을 계산하기 어려움
- 컴퓨터로는 미분계산과정의 구현보다 경사하강법 구현이 더 쉬움
- 데이터 양이 많을 수록 경사하강법이 계산량 측면에서 효율적임
경사하강법의 수식, 유도 및 원리
경사하강법을 유도하는 원리는 아래 사이트가 잘 정리되어 있어 참고했다.
https://angeloyeo.github.io/2020/08/16/gradient_descent.html
파이썬 코드 구현
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(0)
# y = 4X + 6을 근사, 임의의 값은 노이즈를 위해 부여
X = 2 * np.random.rand(100,1) # 0~1 사이의 random 소수
y = 6 + 4*X+ np.random.randn(100,1)plt.scatter(X,y)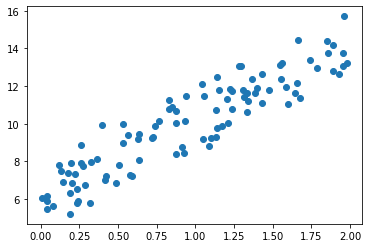
def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost# w1과 w0를 업데이트할 w1_update, w0_update를 반환
def get_weight_updates(w1, w0, X, y, learning_rate=0.01):
N = len(y)
w1_update = np.zeros_like(w1)
w0_update = np.zeros_like(w0)
y_pred = np.dot(X, w1.T) + w0
diff = y - y_pred
w0_factors = np.ones((N,1))
# w1과 w0를 업데이트할 w1_update와 w0_update 계산
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
w0_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
return w1_update, w0_updatedef gradient_descent_stpes(X, y, iters=10000):
# 초기값 0으로 설정
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
# 인자로 주어진 iters 만큼 반복적으로 get_weight_updates() 호출해 w1, w0 업데이트
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate=0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0def get_cost(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N
return cost
w1, w0 = gradient_descent_stpes(X,y, iters=1000)
print(f"w1 : {w1[0,0]:.3f}, w0 : {w0[0,0]:.3f}")
y_pred = w1[0, 0]*X + w0
print("GD Total Cost", round(get_cost(y, y_pred),4))w1 : 4.022, w0 : 6.162
GD Total Cost 0.9935plt.scatter(X,y)
plt.plot(X, y_pred)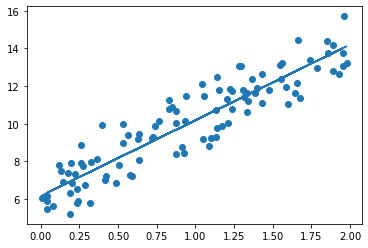
확률적 경사하강법
확률적 경사 하강법(Stochastic Gradient Descent)는 경사 하강법과 다르게 한번 학습할 때 모든 데이터에 대해 가중치를 조절하는 것이 아니라, 램덤하게 추출한 일부 데이터에 대해 가중치를 조절함. 결과적으로 속도는 개선되었지만 최적 해의 정확도는 낮다.
출처: 흰고래의꿈
파이썬 코드 구현
def stochastic_gradient_descent_stpes(X, y, batch_size=10, iters=1000):
w0 = np.zeros((1,1))
w1 = np.zeros((1,1))
prev_cost = 100000
iter_index = 0
for ind in range(iters):
np.random.seed(ind)
# 전체 X,y 데이터에서 랜덤하게 batch_size만큼 데이터 추출하여 sample_X, sample_y로 저장
stochastic_random_index = np.random.permutation(X.shape[0])
sample_X = X[stochastic_random_index[0:batch_size]]
sample_y = y[stochastic_random_index[0:batch_size]]
# 랜덤하게 batch_size만큼 추출된 데이터 기반으로 w1_update, w0_update 계산 후 업데이트
w1_update, w0_update = get_weight_updates(w1, w0, sample_X, sample_y, learning_rate = 0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0w1, w0 = stochastic_gradient_descent_stpes(X, y, iters= 1000)
print("w1 :", round(w1[0,0], 3), "w0:", round(w0[0,0], 3))
y_pred = w1[0, 0]*X + w0
print("Stochastic Gradient Descent Total cost : ",get_cost(y, y_pred))w1 : 4.028 w0: 6.156
Stochastic Gradient Descent Total cost : 0.9937111256675345참고 사이트
'Data > Machine Learning' 카테고리의 다른 글
| PCA(주성분 분석), 고유값, 고유벡터 정리 (0) | 2022.04.12 |
|---|---|
| 차원축소(Dimension Reduction) 정리 (0) | 2022.04.12 |
| Rigdge와 Lasso (0) | 2022.03.31 |
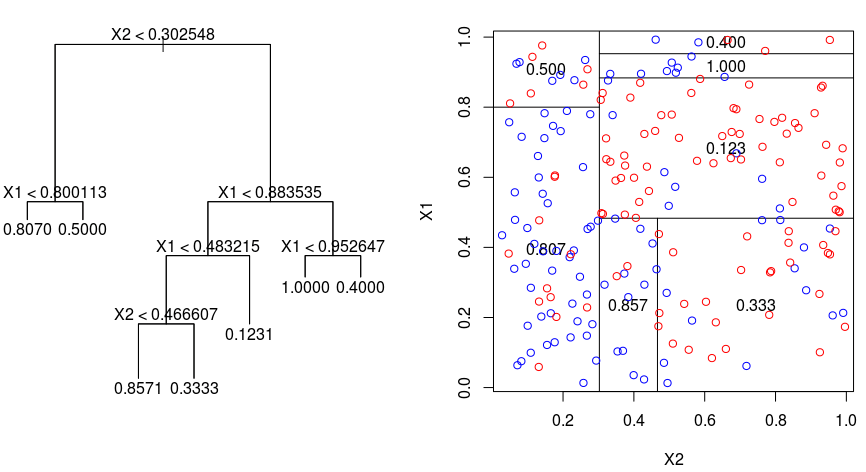
| Decision Tree Regression (0) | 2019.12.27 |
| 파이썬 사이킷런에서 model에서 fit and fit_transform의 차이 (0) | 2019.09.28 |